Divide and Conquer
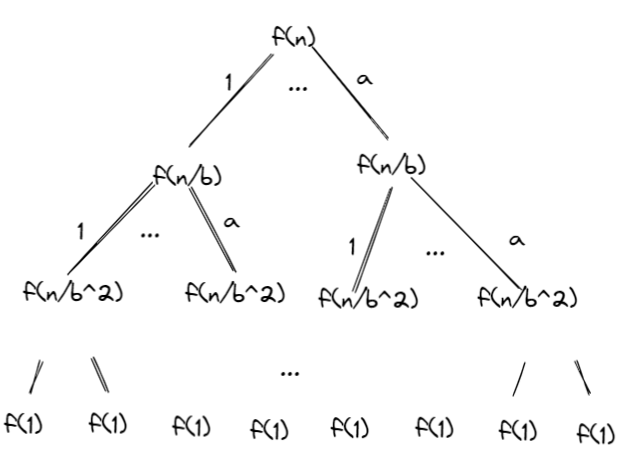
Recursive tree
Master Theory
Form1
The recurrence \(T(N) = aT(N/b) + f(N)\) can be solved as follows:
- If \(af(N/b) = Kf(N)\) for some constant \(K<1\), then \(T(N)=\Theta(f(N))\)
- If \(af(N/b) = Kf(N)\) for some constant \(K>1\), then \(T(N)=\Theta(N^{log_{b}{a}})\)
- If \(af(N/b) = f(N)\), then \(T(N)=\Theta(f(N)log_b{N})\)
Form2
The recurrence \(T(N)=aT(N/b) + \Theta(N^k\log^p{N})\) where \(a\ge 1, b> 1, p\ge 0\):
- \(T(N)=O(N^{\log_b{a}})\), if \(a>b^k\)
- \(T(N)=O(N^k\log^{p+1}{N})\), if \(a=b^k\)
- \(T(N)=O(N^k\log^{p}{N})\), if \(a<b^k\)
Form3
The recurrence \(T(N)=aT(N/b)+f(N)\)
- If \(f(N)=O(N^{\log_b{a}-\varepsilon})\) for some constant \(\varepsilon>0\), then \(T(N)=\Theta(N^{\log_b{a}})\)
- If \(f(N)=\Theta(N^{\log_b{a}})\), then \(T(N)=\Theta(N^{\log_b{a}}\log{N})\)
- If \(f(N)=\Omega(N^{\log_{b}{a}+\varepsilon})\), for some constant \(\varepsilon>0\), and if \(af(N/b)<cf(N)\) for some constant \(c<1\) and all sufficiently large \(N\), then \(T(N)=\Theta(f(N))\)
Special case
求解:\(T(N)=2T(\sqrt{N})+\log{N}\)
\[
\begin{aligned}
&let\ N = 2^m\\
&thus\ T(N)=2T(\sqrt{N})+\log{N}\to T(2^m)=T(2^{\frac{m}{2}})+m\\
&let\ G(m)=T(2^m)\\
&thus\ G(m)=G(m/2)+m \to G(m)=m\log{m}=\log{n}\log\log{n}
\end{aligned}
\]