E-R Model and Normal Form
E-R Model
Basic Concepts
- Entity: The set of permitted values for each attributes
- Relation: A relationship is an association among several entities.
- Weak entity sets: An entity that does not have a primary key is referred to as a weak entity set.
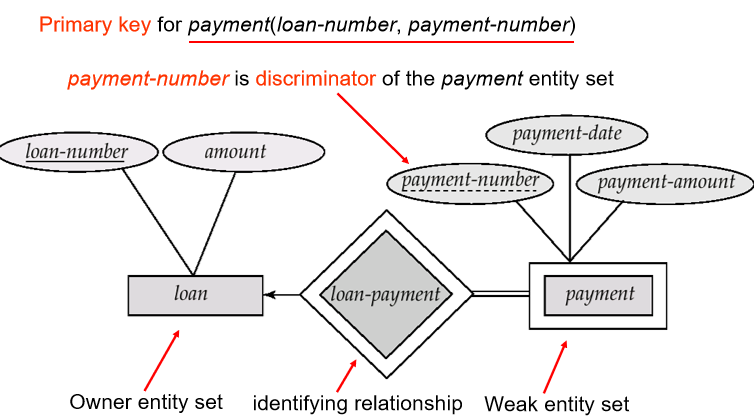
- constraints 约束
- mapping cardinalities 映射基数
- one-to-one
- one-to-many
- many-to-one
- many-to-many
- 参与度约束
- total participation
- partial participation
- key约束
- mapping cardinalities 映射基数
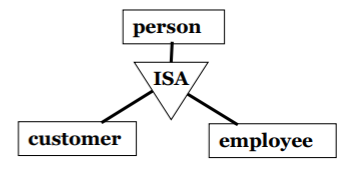
- specialization(特殊化) & generalization(泛化):
- converting Non-Binary Relationships to Binary Form
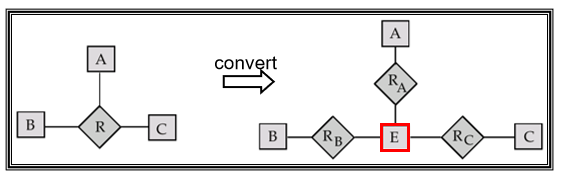
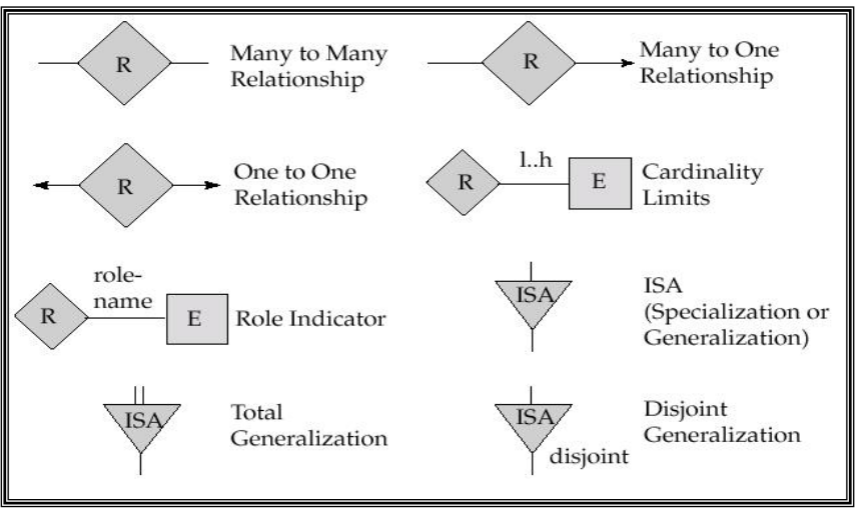
Summary of Symbols
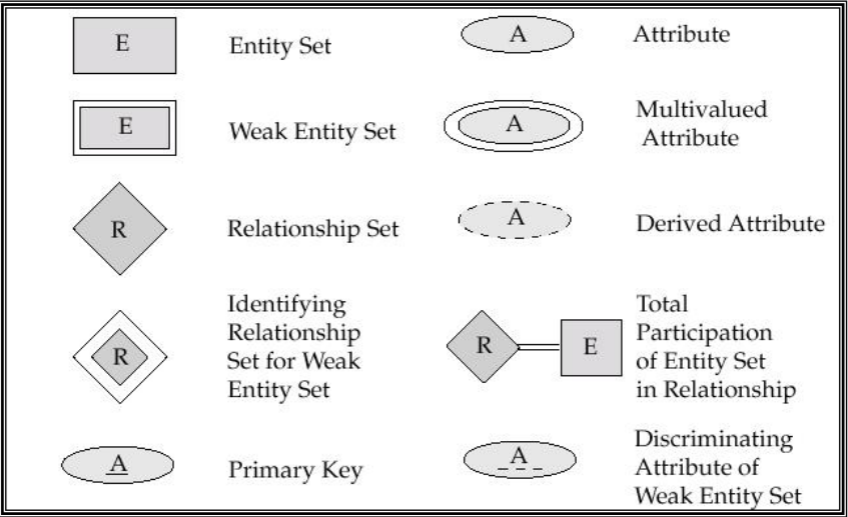
Reduction of an E-R Schema to Tables
(1) Representing Relationshp Sets as Tables
(2) Representing Weak Entity Sets
(3) Redundancy of Tables
1> Many-to-one/one-to-many -> relationship sets add to "many" side
2> one-to-one -> relationship sets add to any side
(4) Representing Specialization as Tables
Normal Form
基本概念
- 分解
- 有损分解(Lossy Decomposition): 不能用分解后的几个关系重建原本的关系,反之为无损分解。
- 无损分解(Lossless Decomposition): \(R_1\cap R_2\)是\(R_1\)或\(R_2\)的超码(充要条件)
- 函数依赖: 对于任何一个一个关系\(R\),若\(\alpha \in R,\beta \in R\),且由\(R\)中两个元组\(t_1,t_2\)中的\(\alpha\)属性值相同可以得出其\(\beta\)属性值相同,则称\(\alpha\to \beta\)是一个函数依赖,即\(\alpha\)可以唯一标识/决定\(\beta\)。若\(R\)中的每个元组都满足函数依赖,则称函数依赖在\(R\)上成立。
- 平凡的函数依赖:\(\alpha \subset \beta\) 推出 \(\beta \to \alpha\)
- \(K\)是\(R\)的超码\(\iff K\to R\)
- 闭包:由给定的函数依赖\(F\)所能推导出的所有函数依赖构成的集合\(F^{+}\)
- Armstrong公理

- 属性集闭包:某属性所能唯一决定的属性的集合
- Armstrong公理
- 无关属性:如果去除函数依赖中的某个属性不会改变这个函数依赖集的闭包,则称该属性是无关的。
- 最小覆盖:最小覆盖\(F_c\)必须满足(1)\(F_c\)中任何函数依赖不含无关属性。(2) \(F_c\)中任何函数左半部分唯一
- 寻找最小覆盖的方法
- 令\(F_c=F\).
- 利用合并律将所有\(\alpha\to\beta_1,\alpha\to\beta_2,\dots\)合并为\(\alpha\to\beta_1\beta_2...\)
- 在\(F_c\)中寻找一个具有无关属性的函数依赖,并删除该无关属性。
- 重复上述步骤直至\(F_c\)不变
- 依赖保持分解:令\(F\)为\(R\)上的一个函数依赖集,\(R_1,R_2,\dots,R_n\)是\(R\)的分解,用\(F_i\)表示只包含\(R_i\)中出现的元素的函数依赖的集合,若\((F_1\cup F_2\cup\dots\cup F_n)^{+}=F^{+}\),则该分解为依赖保持分解。
第一范式
所有属性都是原子的(atomic),即不可再细分的。
BC范式
- Boyce-Codd Normal Form
- 性质:任意函数依赖\(\alpha\to\beta\)至少满足下面任意一项
- \(\alpha\to\beta\)是平凡的
- \(\alpha\)是\(R\)的一个超码
- 判断函数依赖\(\alpha\to\beta\)是否违反了BCNF:计算\(\alpha^{+}\),若其既不是\(\beta\)(平凡的),也不是所有元素的集合(不是超码),则不是BCNF
- BCNF分解(同时也是无损分解)
- Suppose we have a schema R and a non-trivial dependency \(\alpha \to \beta\) causes a violation of BCNF.We decompose R into: \((\alpha \cup \beta)\) and \((R-(\beta-\alpha))\)
第三范式
- 3rd Normal Form
- 性质:任意函数依赖\(\alpha\to\beta\)至少满足下面任意一项
- \(\alpha\to\beta\)是平凡的
- \(\alpha\)是\(R\)的一个超码
- \(\beta-\alpha\)中的每个属性A都包含于\(R\)的候选码中
- 任何BCNF范式都是3NF范式
- 3NF分解

- 相比之下,3NF分解可以保证依赖保持,而BCNF不一定
- BCNF和3NF都能保证无损分解