Splay Trees

Definition

Any \(M\) consecutive tree operations starting from an empty tree take at most \(O(M\log N)\) time.

Rotation

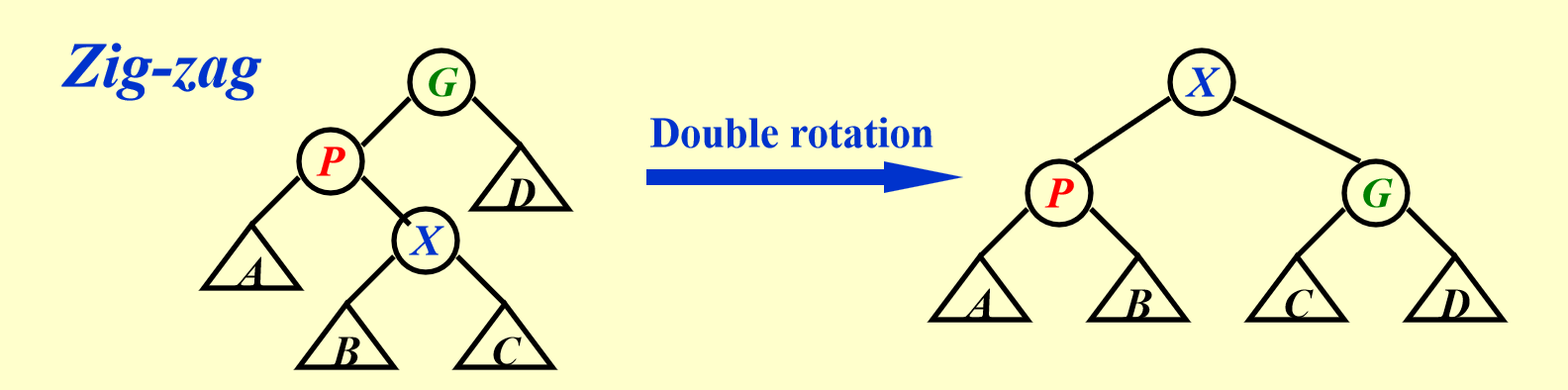
• zig-zag
  • 
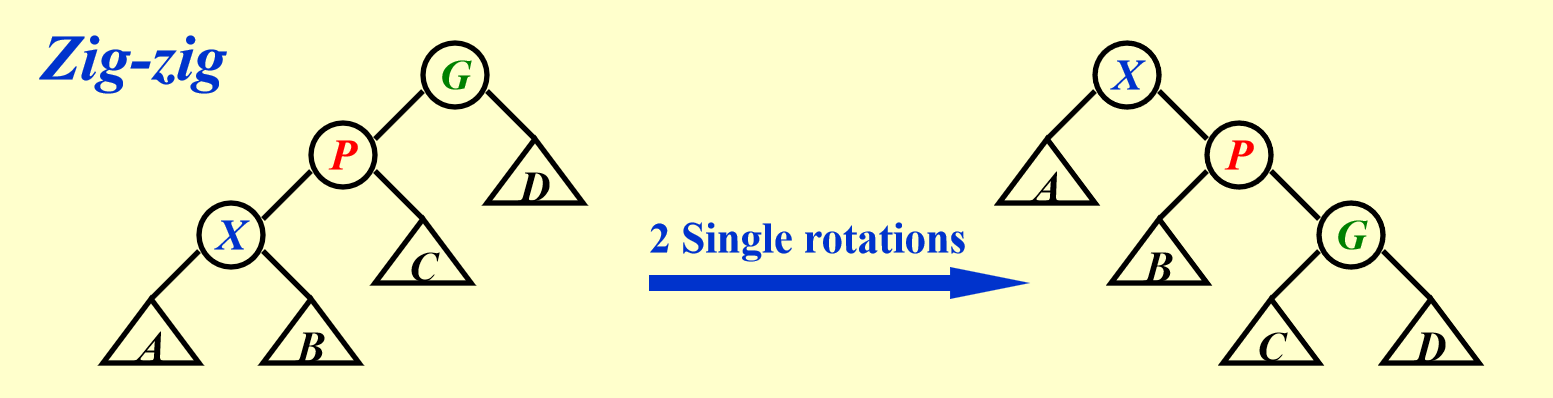
• zig-zig
  • 

Analysis

Let \(\Phi(T)=\sum\limits_{i\in T}\log{Size(i)}\) According to \(\hat{c_i} = c_i + \Phi(T) - \Phi(T_{{\rm before}})\) Moreover, we can proof that

\[ \begin{aligned} Zig&: \hat{c_i}=c_i+\Phi(T)-\Phi(T')=1+R_2(X)-R_1(X)+R_2(P)-R_1(P)\le 1+R_2(X)-R_1(X)\\ Zig-Zag&: \hat{c_i}=c_i+\Phi(T)-\Phi(T')=2+R_2(X)-R_1(X)+R_2(P)-R_1(P)+R_2(G)-R_1(G)\le 2(R_2(X)-R_1(X))\\ Zig-Zig&: \hat{c_i}=c_i+\Phi(T)-\Phi(T')=2+R_2(X)-R_1(X)+R_2(P)-R_1(P)+R_2(G)-R_1(G)\le 2(R_2(X)-R_1(X))\\ \end{aligned} \]

Thus, the amortized time to splay a tree with root \(T\) at node \(X\) is at most \(3(R(T)-R(X))+1=O(\log{N})\)