Red-Black Trees

Definition

• Every node is either red or black
• The root is black
• Every leaf(NIL) is black
• If a node is red, then both its children are black
• For each node, all simple paths from the node to descendant leaves contain the same number of black nodes

Lemma

• A red-black tree with n internal nodes has height at most \(2\ln(N+1)\)
• Proof $$ \begin{aligned} {\rm sizeof}(x) &= 1+2{\rm sizeof}(child)\ &\ge 1+2\cdot2^{bh(child)}\ &\ge 1+2\cdot2^{bh(x)-1}\ &\ge 1+2\cdot2^{h(x)/2-1}\ h(x)/2-1 &\le\ln(({\rm sizeof}(x)-1)/2) \le\ln({\rm sizeof }(x))\ h(x) &\le 2\ln({\rm sizeof(x)})+1 \end{aligned} $$

Insert

• the initial color of the node is red

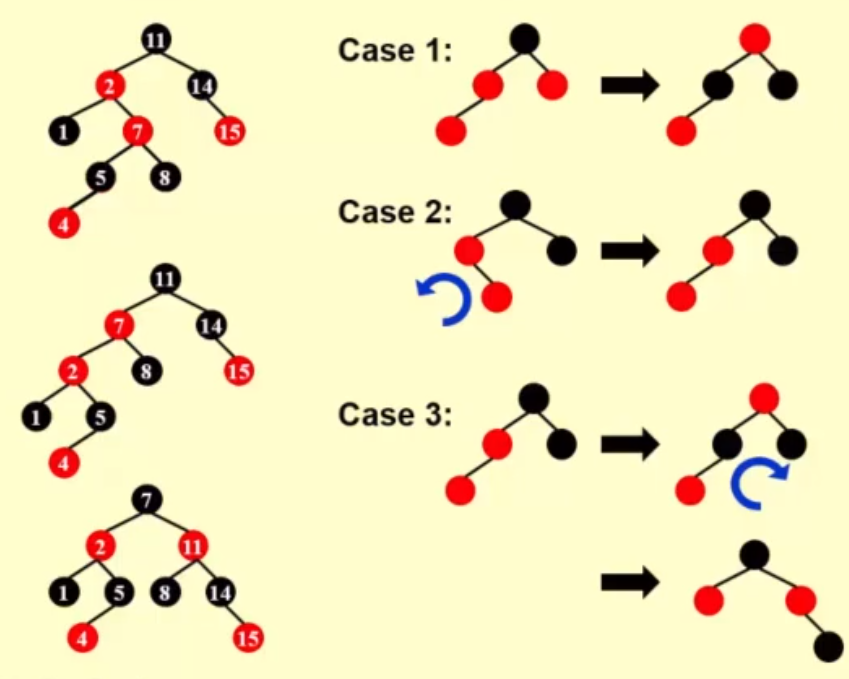
Delete

• Delete a leaf node: Reset its parent link to NIL
• Delete a degree 1 node: Replace the node by its single child
• Delete a degree 2 node: Replace the node by the largest one in the left subtree or the smallest one in the right subtree.
• the number of rotations in the DELETE operation is \(O(1)\).红黑树在Insert中旋转次数不超过2，删除的过程中旋转次数不超过3

How to Replace

Accoring to the three situations, the second and third situation can be transfomed into situation 1. Therefore, we only need to care about situation1 -- how to delete a leaf node. Unfortunately, we can't delete leaf node directly, for the existence of external nodes.

• case1
• case2
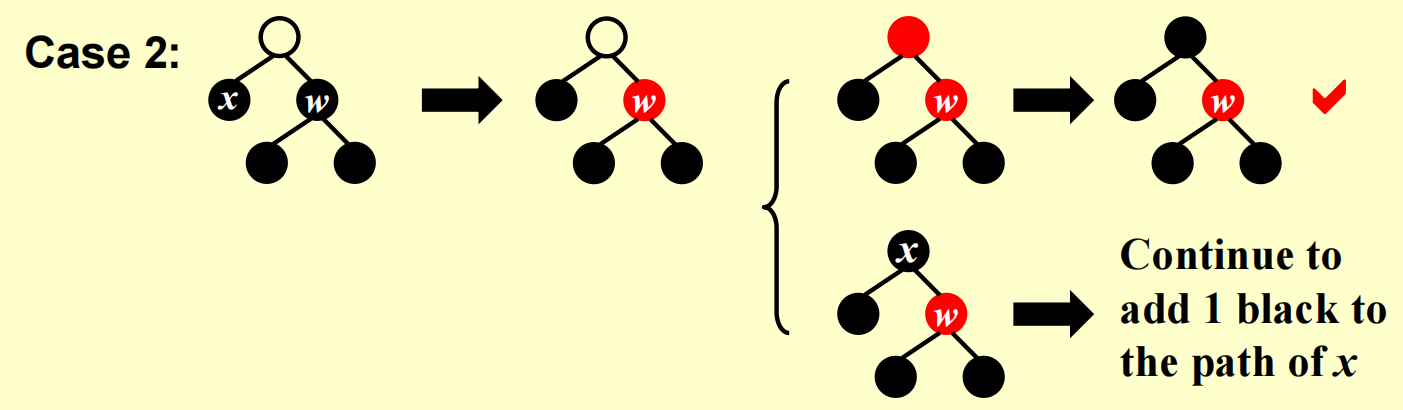
• case3
• case4