Binomial Queue

Definition

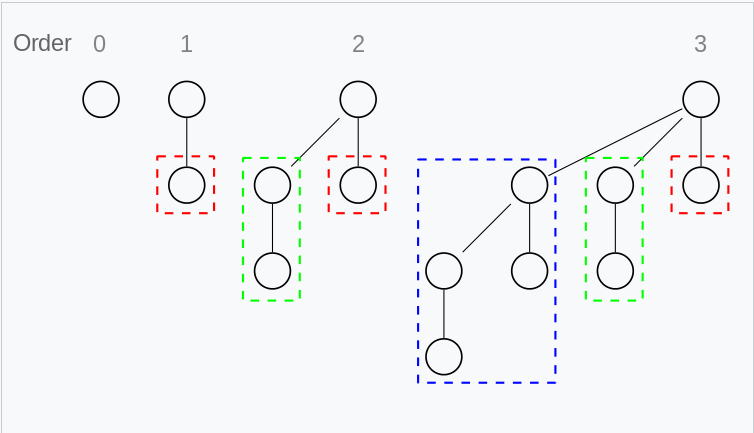
Character

for \(B_k\)

• has exactly \(2^k\) nodes
• the number of nodes at depth \(d\) is \(\binom{k}{d}\)

for a priority queue of size \(13\)

• \(13 = 2^0 + 0\times 2^1 + 2^2 + 2^3 = 1101_2\)

A binomial queue of \(N\) elements can be built by \(N\) sccessive insertions in \(O(N)\) time.

Operation

FindMin

There are at most \(\lceil \log{N}\rceil\) roots, hence \(T_p = O(\log{N})\)

Merge

\(T_p = O(\log{N})\)

DeleteMin

\(T_p=O(\log{N})\)

Decreased Key

\(T_p=O(\log{N})\)