AVL Trees

Adelson-Velskii-Landis[AVL] Trees

Definition

• The balance factor BF(node) = \(h_L - h_R\).
• In an AVL Tree, BF(node) = -1, 0, 1.

Different Trees

• Perfect Binary Tree
• Complete Binary Tree
• Full Binary Tree: has two leaf nodes or not. e.g. Huffman Tree

Rotation

• LL Rotation/RR Rotation

  • Two Single Rotation
  • 
  • 

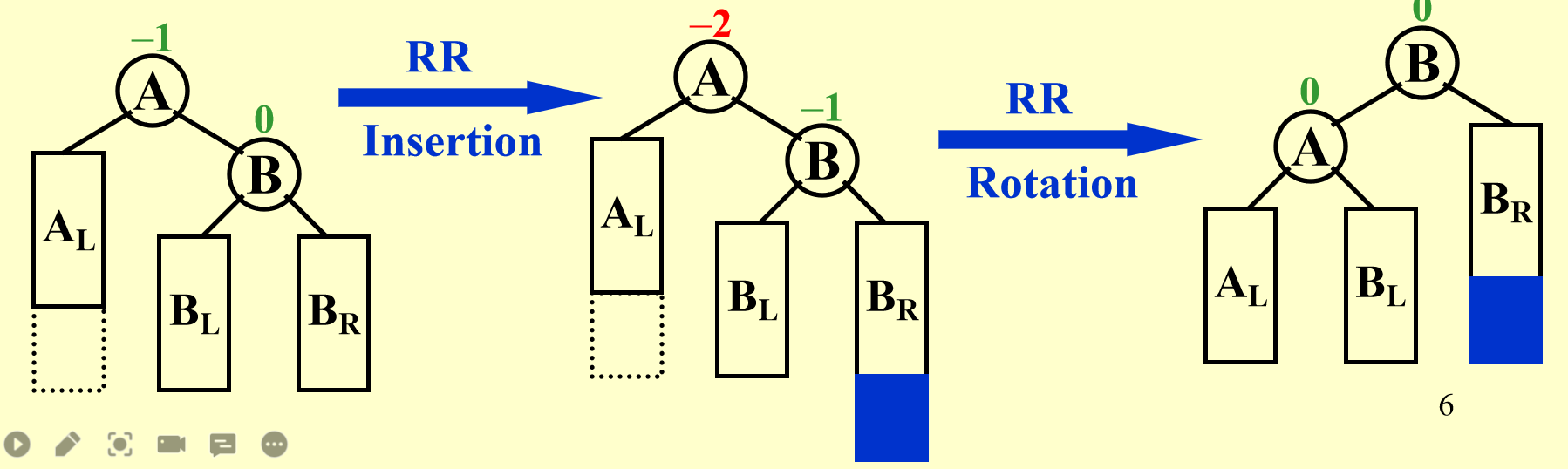
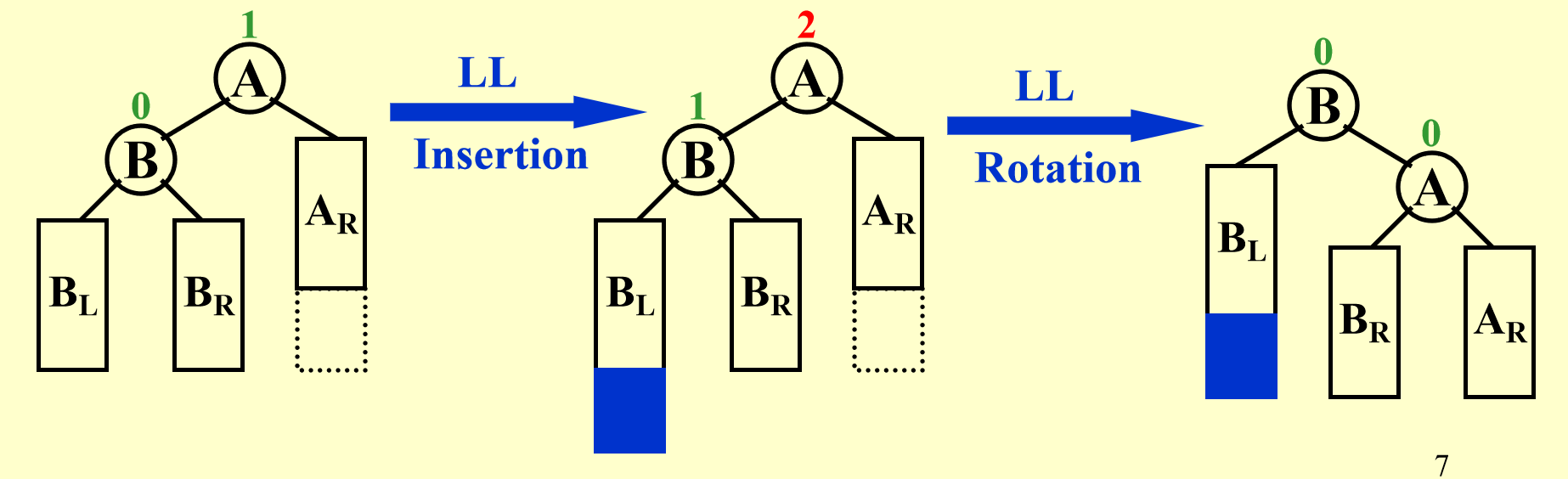
• LR Rotation/RL Rotation

  • Double Rotation
  • 
  • 

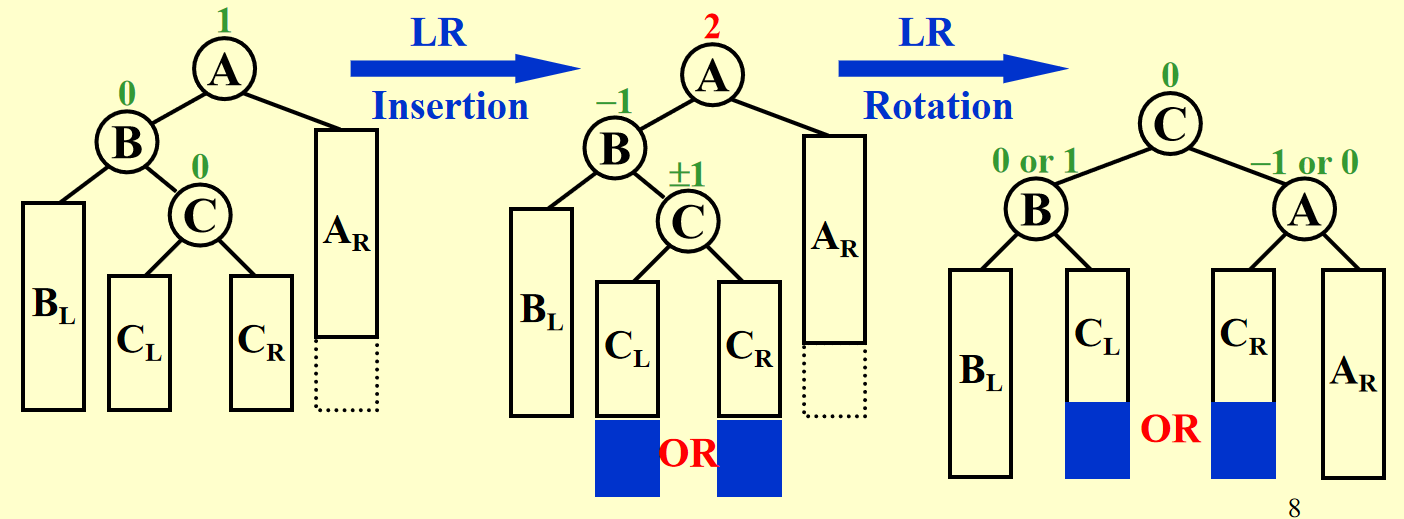
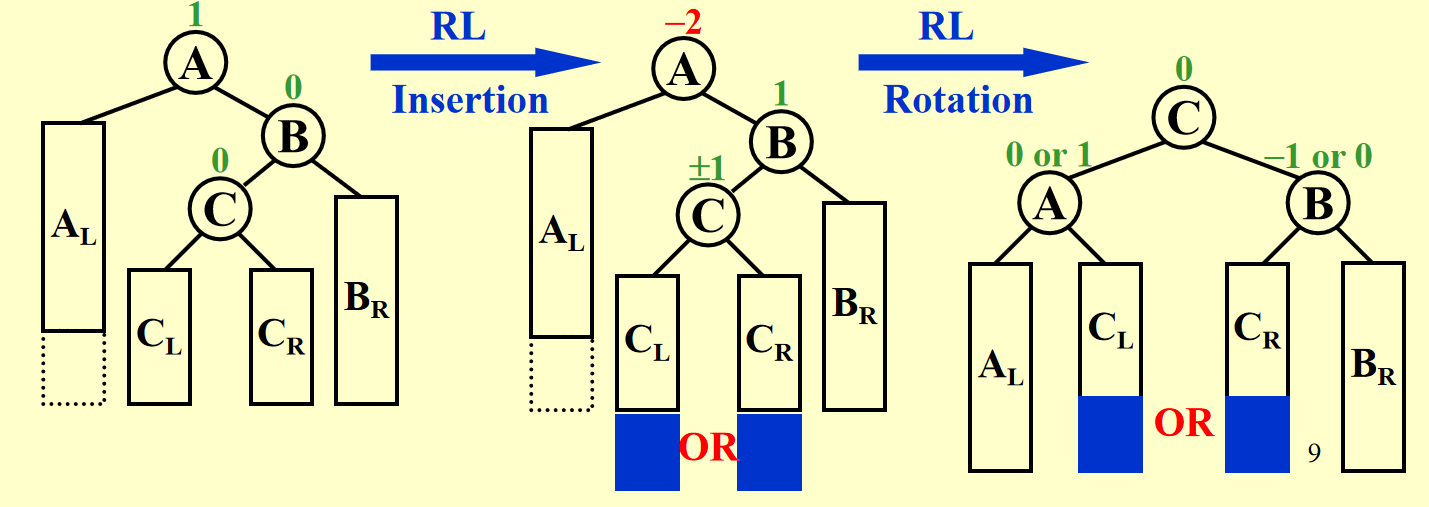
Analysis

Let \(n_h\) be the minimum number of nodes in a height balanced tree of height \(h\)

\[ \begin{aligned} n_h &= n_{h-1} + n_{h-2} + 1\\ (n_h + 1) &=(n_{h-1}+1)+(n_{h-2}+1)\\ F_h &= F_{h-1} + F_{h}\ [F_{h+2} = n_h + 1,F_3=2=n_1+1]\\ F_h&\approx\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^h\\ n_h&\approx\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^{h+2}-1\\ h&=O(\ln{n}) \end{aligned} \]